- 팩토리얼
팩토리얼은 !으로 표현하는데 n!은 1부터 n보다 작거나 같은 모든 자연수의 곱이다.(*0!=1이다.)
n!= 1×2×···×(n-1)×n
n!은 n명을 1자로 줄 세울 수 있는 경우의 수와 같다.
첫 번째 자리에 올 수 있는 사람 n명, 두번째 자리에 올 수 있는 사람은 첫번째 자리에 간 1사람을 제외한 n-1명, 이와 같은 과정을 반복하면 n-1번째 자리에 올 수 있는 사람은 2명, n번째 자리에 올 수 있는 사람은 1명이다. n명을 1자로 줄 세울 수 있는 경우의 수는 이를 모두 곱한 값과 같으므로 n!과 같음을 알 수 있다.
- 순열
순열은 서로 다른 n개의 물건 중 r개를 선택하여 나열하는 경우의 수이다. nPr의 형태로 표현한다. 이를 팩토리얼로 나타내보자.
첫번째 자리에 올 수 있는 물건은 n개, 두번째 자리에 올 수 있는 물건은 첫번째 자리에 놓은 1개를 제외한 n-1개, 이와 같은 과정을 반복하면 r-1번째 자리에 올 수 있는 물건은 n-r+2개, n번째 자리에 올 수 있는 물건은 n-r+1개이다. n개의 물건 중 r개를 선택하여 나열하는 경우의 수는 이를 모두 곱한 경우의 수와 같으므로

이다.
- 조합
조합은 서로 다른 n개의 물건 중 r개를 선택하는 경우의 수이다. nCr의 형태로 표현한다. 이를 팩토리얼로 표현해 보자.
nCr에서 뽑은 r개를 배열하면 nPr이므로 r!×nCr=nPr임을 알 수 있다. 따라서
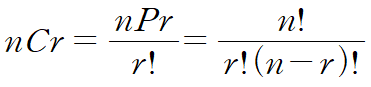
이다.
- 교란순열의 일반항
이전글에서 교란순열의 점화식을 구했는데 조합과 순열, 포함배제의 원리를 이용하여 교란순열의 일반항을 구해보자.
n명의 사람의 모자가 섞인 후 다시 모자를 썼을 때 나올 수 있는 경우의 수는 n!이다.
이 경우를 Dn과 1명 이상이 자신의 모자를 썼을 경우로 나누어 보자.
1명이상이 자신의 모자를 썼을 경우를 계산해 보면, 1명이 자신의 모자를 썼을 경우의 수는 nC1X(n-1)!인데 이 경우에서는 중복된 경우가 생긴다. 포함배제의 원리에 의해 짝수명이 자신의 모자를 썼을 경우의 수는 빼고 홀수명이 자신의 모자를 썼을 경우의 수는 더해줘야 한다.
이를 식으로 바꿔보면
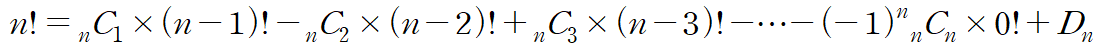
가 된다. 여기서 nCk꼴을 팩토리얼로 바꿔보면

이 되는데 우변에서 Dn을 제외한 나머지 항을 약분해서 간략하게 만든 다음에 이항하고 n!으로 묶어주면
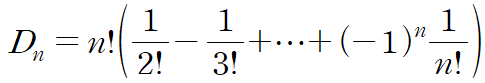
이 된다. 물론 점화식에서 일반항을 유도하는 방법도 있으나 그것은 여기에서 다루지 않겠다.