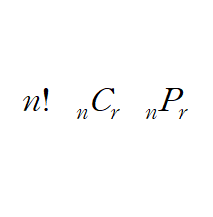In-Game 밤송이에 닿자마자 다시 터치해 바로 밤송이를 통과하는 기술, 이른바 ' 밤캔'(밤송이 캔슬)에 대한 보너스 점수를 부여했습니다. 벽면의 다람쥐를 튕기게 하는 기능이 항상 균일한 속도로 작용하지 않는 문제를 내적 매커니즘을 수정함으로써 해결했습니다. 포탈 안에 포탈이 생성되는 버그, 포탈에 도토리가 나오지 않는 버그 등을 수정했습니다. 하드 난이도의 배경 맵을 수정했습니다. UI 게임 최초 실행 후 첫 보너스 점수 표기 시 렉이 발생하는 버그를 해결한 줄 알았습니다. 저희는 멀었나 봅니다..흑흑 보너스 점수가 사라질 때 페이드아웃됩니다. 아이콘을 만들었습니다. Later 홈 버튼 클릭 후 다시 게임에 진입1 시 일시정지 화면이 표시되게 할 것입니다. 일시정지 버튼을 누를 때 인게임 터치에 영..