롤의 정리는 증명이 간단하면서도 평균값 정리나 로피탈의 정리 등 다양한 정리들의 증명에 잘 사용되니 알아두시면 유용하리라 기대됩니다. 롤의 정리의 증명에는 페르마의 정리가 사용되는데, 이것은 이전 글에 증명해 두었습니다.
롤의 정리는 다음과 같습니다.

즉, 함수 f가 다음 세 조건을 만족할 때,
- f가 닫힌구간 [a, b]에서 연속이고
- f가 열린구간 (a, b)에서 미분가능하며
- f(a) = f(b).
f'(c)=0을 만족하는 c가 열린구간 (a, b)에 존재한다는 의미입니다.
세 가지 경우로 나누어서 증명하겠습니다.
1. f(x) = k, 상수일 때 (f가 상수함수일 때)
열린구간 (a,b) 전체에서 f'(x)=0이므로, c에는 구간 내의 아무 값이나 가져와도 롤의 정리에 부합합니다.
2. 열린구간 (a, b)에 속하는 어떤 x에 대해, f(x) > f(a)일 때
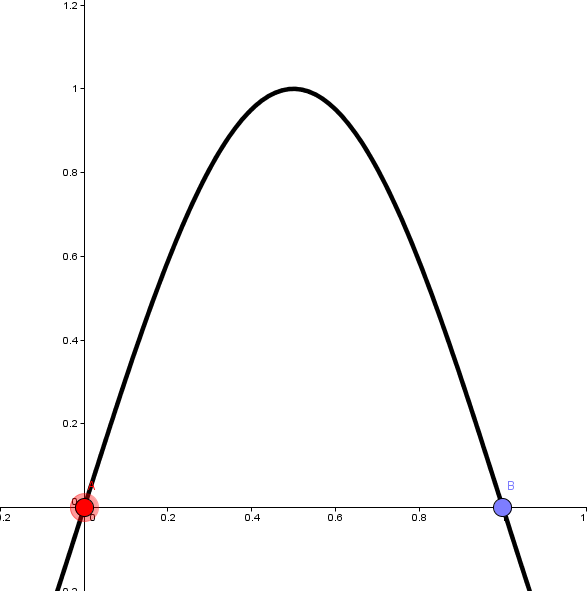
f가 조건에 의해 닫힌구간 [a, b]에서 연속이므로, 최대·최소 정리에 의해 f는 [a, b]에서 최댓값 f(c)를 갖습니다.
그런데 조건에 의해 f(a)=f(b)이고, f(x)>f(a)를 만족하는 어떤 x가 열린구간 (a,b)에 존재하므로, c는 최소한 a나 b는 아닐 것입니다.
다시 말해 f는 (a, b)에서 최댓값 c를 가집니다. (닫힌구간이 열린구간으로 바뀐 것을 알 수 있습니다!)
그러면, f가 c에서 극댓값을 가지며(모든 최댓값은 극댓값입니다. 이전 글에서 설명한 정의를 잘 살펴보면 알 수 있습니다.),
조건에 의해 f는 (a,b)에서 미분가능하므로,
페르마의 정리에 의해 f'(c)=0입니다.
3. 열린구간 (a, b)에 속하는 어떤 x에 대해, f(x) < f(a)일 때
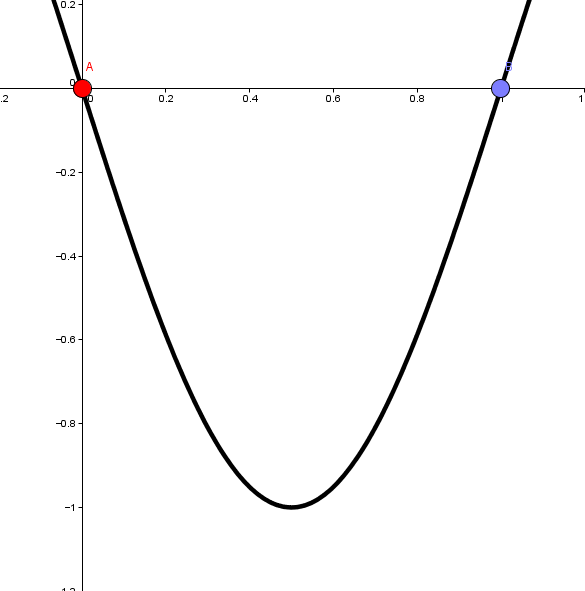
2번 경우에서 부호만 반대이고 비슷합니다.
f가 [a, b]에서 연속이므로, 최대·최소 정리에 의해 f는 [a, b]에서 최솟값 f(c)를 갖습니다.
그런데 f(a)=f(b)이고, f(x)<f(a)를 만족하는 어떤 x가 (a,b)에 존재하므로, c는 a나 b와는 같아질 수 없습니다.
즉 f는 (a, b)에서 최솟값 c를 가집니다.
그러면, f가 c에서 극솟값을 가지며 조건에 의해 f는 (a,b)에서 미분가능하므로, 페르마의 정리에 의해 f'(c)=0입니다.

물론 위와 같은 경우에서도 똑같습니다. 다만 2번 경우와 3번 경우를 둘 다 만족하고 있을 뿐입니다.
자연스럽게 f'(c)=0을 만족하는 c의 값으로 가능한 것도 최소 두 가지 이상이 보장되겠죠.
다음 글에서는 이번에 증명한 롤의 정리를 이용하여 평균값 정리를 증명하겠습니다.
'Lecture > Calculus' 카테고리의 다른 글
| 미적분의 기본정리 1 증명 (F.T.C. 1) (0) | 2023.01.29 |
|---|---|
| 연속성의 정의와 관련 정리들의 증명 총정리 (1) | 2023.01.25 |
| 평균값 정리 증명 (Mean Value Theorem) (0) | 2023.01.24 |
| 페르마의 정리 증명 (Fermat's Theorem) + 최대, 극대, 임계값의 개념 (1) | 2023.01.23 |
| 극한 법칙의 엄밀한 증명(엡실론-델타 논법) - 합과 차의 법칙 (0) | 2023.01.23 |