함수 f가 a에서 연속임은 다음과 같이 정의됩니다.

이 정의는, f가 a에서 연속이기 위해서 다음 세 조건이 요구됨을 알려줍니다.
- f(a)가 정의된다.(a가 f의 정의역에 속한다.)
- x가 a로 접근할 때의 f(x)의 극한값이 존재한다.
- 1에서의 f(a)가 2에서의 극한값과 같다.
한편, 한쪽 방향의 극한값만이 함숫값과 같다면, 그 방향으로만 연속입니다.
다시 말해,

물론 좌극한과 우극한이 같으면 완전히 연속입니다.
그렇다면 어떤 구간에서 f가 연속임은 어떻게 정의될까요?
간단하게, 구간 내의 모든 점에서 연속이면 f가 그 구간에서 연속이라고 합니다.
열린구간이면 문제될 게 없지만, 닫힌구간이면 양 끝점이 문제가 됩니다.
비유해봅시다. 줄넘기 줄이 끊기지 않고 한 줄로 연결돼있음을(연속임을) 어떻게 표현할까요? 줄넘기 줄의 작은 부분을 봤을 때, 그 부분의 왼쪽에도 오른쪽에도 줄이 이어져있으면 됩니다. 그런데 줄넘기의 양쪽 끝은 그렇지 않겠죠. 둘 중 한쪽은 오른쪽만, 한쪽은 왼쪽만 이어져 있습니다. 그래도 줄넘기 줄은 연속입니다.
구간에서도 양 끝점은 한쪽 방향으로만 연속이면 됩니다. 구간의 양 끝점 중 왼쪽의 점은 오른쪽으로 연속, 오른쪽의 점은 왼쪽으로 연속이면 됩니다.
이제 몇 가지 연속성에 관련된 정의들을 살피겠습니다.
먼저, Chapter 1에서 나왔던 극한 법칙을 다시 상기하고 가겠습니다.

위의 법칙은 참임을 증명할 수 있습니다.
그렇다면 우리는 한 가지 사실을 알 수 있습니다.
x가 a로 접근할 때 함수 f와 g의 극한값이 각각 f(a), g(a)와 같다면, (= f와 g가 a에서 연속이라면,)
- f(x)±g(x)의 극한값은 f(a)±g(a)이다. (= f±g도 a에서 연속이다.)
- cf(x)의 극한값은 cf(a)이다. (= cf도 a에서 연속이다.)
- f(x)g(x)의 극한값은 f(a)g(a)이다. (= fg도 a에서 연속이다.)
- f(x)/g(x)의 극한값은 f(a)/g(a)이다. (= f/g도 a에서 연속이다.)
쉽게 말해,
'f와 g의 극한값이 (요거요거)이면, 모시깽이 함수의 극한값은 (죠거죠거)가 된다.'
라는 Chapter 1의 극한 법칙에서,
'f와 g가 연속이면, 모시깽이 함수는 연속이다.'
로 바꾸기만 하면 됩니다. 물론, 나눗셈을 포함한 법칙에서는 분모가 0이 되는 경우를 제해야겠죠.
그런데 위 정리를 쓰려면 의문이 듭니다.
f와 g가 연속이면 f+g도 연속이라는 건 알겠는데, 애초에 f와 g가 연속인 것은 어떻게 알까.
그래서 우리는 아래 정리를 기억해 두어야 합니다.
- 모든 다항함수는 정의역(= 실수 전체)에서 연속이다.
- 모든 유리함수는 정의역(= 분모가 0이 되는 점을 제외한 실수 전체)에서 연속이다.
이것 또한 증명해보겠습니다.
먼저 모든 다항함수는 아래와 같이 표현할 수 있습니다.

한편, 우리는 상수의 극한값은 그냥 원래 상수와 같음을 알고,
(엡실론-델타 논법으로 쉽게 증명할 수 있습니다. lim{x→a} (c) = c임을 즉석으로 증명하자면,
ε이 애초에 양수이기 때문에, δ를 무엇으로 잡더라도 0<|x-a|<δ일 때 |c-c|=0<ε임이 자명합니다.)

m이 자연수라면 위 또한 성립함을 알 수 있습니다.
(물론 위 등식은 모든 실수 m에 대해 성립하지만, 자연수 m에 대해 성립하는 것만 보여도 이 증명에서는 충분합니다.
Chapter 1에서 등장한 곱의 극한 법칙(f(x)g(x)의 극한값은 f(a)g(a), f와 g 자리에 모두 x를 집어넣자.)을 m-1번 사용하면 됩니다.
물론, lim{x→a} (x) = a라는 것 정도는 증명해야 합니다. δ=ε으로 잡으면 됩니다.)
그러면 모든 실수 a에 대해, 다음이 성립함을 알 수 있겠죠.

(먼저 양변 전체에 lim을 씌우고, 합의 극한 법칙을 사용해 우변의 모든 항에 각각 lim을 덧붙이고, 우변에서 상수항을 제외한 나머지 항들은 상수배의 극한 법칙을 사용해 계수를 lim 앞으로 뺍니다. 그러면 아까 언급한 두 가지 사실에 의해 위 식이 나옵니다.)
다항함수가 정의역에서 연속임을 보였으면, 유리함수가 정의역에서 연속임을 보이는 것은 쉽습니다.
유리함수 f(x)는 P(x)/Q(x) 형태로 표현할 수 있습니다. P(x)와 Q(x)는 다항함수겠죠? 따라서 앞서 보였듯 둘 다 실수 전체에서 연속입니다.
한편, f(x)의 정의역은 Q(x)≠0인 모든 실수 x입니다.
이 정보들을 다른 말로 표현해보겠습니다. f의 정의역에 속하는 모든 실수 a에 대해,

위와 같이 성립합니다. 어디서 많이 본 조건인데, 바로 곱의 극한 법칙의 조건입니다. 이 법칙에 의해 아래가 성립합니다.

P(x)/Q(x)는 다름 아닌 f(x)이고, 즉 x가 a로 접근할 때의 f(x)의 극한값이 f(a)와 같다는 의미죠.
다시 말하지만 정의역에 속한 모든 실수 a에 대해서입니다.
따라서 연속의 정의에 의해, 유리함수 f는 정의역에서 연속입니다.
한편 이 밖에도, 제곱근 함수, 삼각함수 등도 정의역 전체에서 연속입니다.
제곱근 함수는 그렇게 증명이 어렵지는 않을 것 같습니다.

아까 전 다항함수 증명에 썼던 녀석인데, 아까도 언급했지만 사실 자연수뿐만 아니라 모든 실수 m에 대해 성립합니다.
실수 m에 대해 증명하는 것은 좀 더 복잡한 과정을 거치겠지만, 유리수 m에 대해 증명하는 것은 기본 극한 법칙들을 잘 사용하면 됩니다.(m을 p/q(q≠0, p와 q는 정수)꼴로 두어야겠죠.)
삼각함수는 증명이 조금 더 까다롭습니다. 삼각함수가 연속인 것을 보이기 전에, 이것부터 증명하고 갑시다.
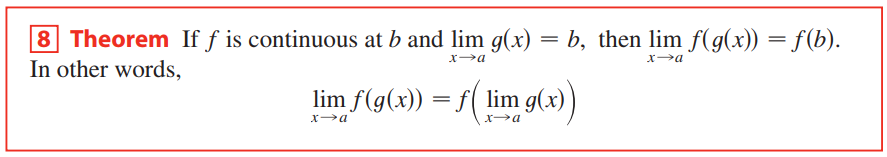
f가 b에서 연속이고, x가 a로 접근할 때 g(x)의 극한값이 b이면, 저기 저 두번째 줄이 성립한다는 뜻입니다. 이건 엡실론-델타 논법으로 증명하겠습니다.
먼저 f가 b에서 연속이므로 b로 접근하는 극한값이 b에서의 함숫값과 같고, 이를 극한의 엄밀한 정의로 표현하면 아래와 같습니다.
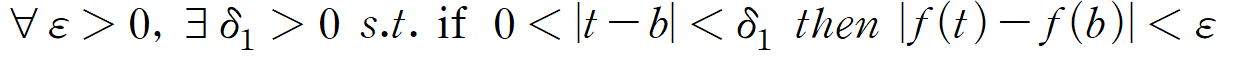
또, lim{x→a}g(x) = b이므로, 이를 극한의 엄밀한 정의로 표현하면 아래와 같습니다.

이번엔 모든 양의 실수 엡실론이 아닌 것에 주목합시다. 모든 양수 엡실론에 대해 성립한다는 것은, 다르게 말하면, 우리가 증명을 위해 엡실론의 값을 임의로 특정해 줘도 된다는 뜻입니다. 이미 g(x)의 극한이 b임을 알고 있기에 이 방법이 가능합니다.
그러면 신기한 일이 벌어집니다. 만약 0<|x-a|<δ이면, |g(x)-b|<δ₁이 성립하고, 그러면 |f(g(x))-f(b)|<ε이 성립합니다.
(t 자리에 g(x)가 대입된 것입니다.)
어느덧 극한의 엄밀한 정의에 의해 이 정리가 증명되었습니다.
그리고 마치, 아까 전 기본 극한 법칙들을 이용해 연속에 관한 정리를 만들어낸 것처럼, 이 정리도 연속성에 대한 따름정리를 야기합니다.
방금 그 정리에 의해, g(x)가 a에서 연속이고 f(x)가 lim{x→a}g(x)에서 연속이라면,
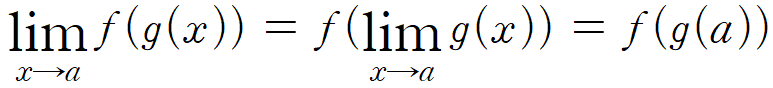
엇, f(g(x))도 a에서 연속이네요!
드디어드디어 모든 삼각함수가 정의역에서 연속임을 증명합시다.
근데 진짜 마지막으로 하나만 알고 가자면, 제일 처음 설명한 연속의 정의를 이렇게도 표현할 수 있다는 것입니다.

이것을 만족하면 f는 a에서 연속입니다. 빠르게 증명하겠습니다.

잠시 원래 정의를 가져왔습니다. 이 정의를 엡실론-델타 논법으로 표현하면 다음과 같습니다.

여기서 h=x-a로 두면 위 문장은 다시 이렇게 표현됩니다.
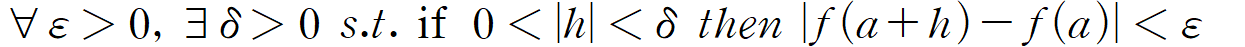
그러니, 다시 극한의 엄밀한 정의에 의해 처음 그 식이 성립하는 걸 알 수 있겠죠? 증명 끝.
이제 사인함수부터 갑시다. 사인함수가 정의역에서 연속인 걸 보이려면 정의역에 속하는 모든 실수 x에 대해 다음이 성립하는 것만 보이면 됩니다.
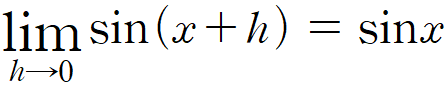
이 식은 삼각함수의 덧셈정리에 의해, 다시 이렇게 표현됩니다.
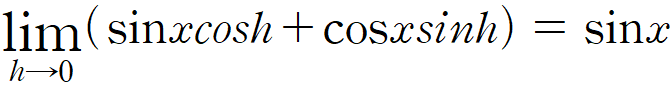
다시 상수배와 합의 극한 법칙에 의해, 이렇게 쪼개지리라 기대합니다.
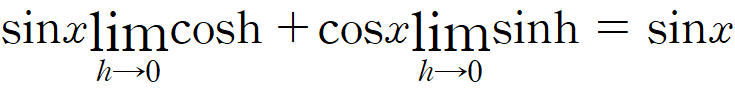
물론 바로는 못 쪼갭니다. cosh와 sinh의 극한을 알고 있어야 쪼갤 수 있습니다. 너무 직관적으로 1과 0이지만, 아쉽게도 그렇게 바로 가지는 못합니다.
이거 일이 커졌는데요. 나눠서 올릴 걸 그랬나
0<x<π/2에서 x > sinx라는 사실 아시겠죠.? 어... 죄송합니다 증명할게요...

기하적 증명으로 타협을 보겠습니다. 반지름의 길이가 1이고 중심각이 x인 부채꼴를 생각하면, 위와 같이 x>sinx임을 알 수 있습니다.
x>π/2일 때는 어떨까요? x>π/2>1≥sinx 입니다.
즉, 양의 실수 x에 대해 x>sinx입니다.
음의 실수 x에 대해서는 어떨까요?
x와 sinx는 기함수입니다.(Chapter 1 참고)
따라서, -x>sin(-x)이므로, -x>-sinx입니다.
x가 0일 때에는 sinx=x=0입니다.
우리는 방금, 모든 실수 x에 대해 |x|≥|sinx|라는 절대부등식을 증명해버렸습니다.
이제야, lim{h→0}sinh = 0임을 쉽게 보일 수 있겠군요. 그냥 모든 양의 실수 ε에 대해, δ도 ε이랑 똑같이 잡아주면,
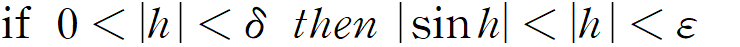
끝! 극한의 엄밀한 정의.

범위 내에서 cosx는 양수니까 문제없어 보입니다.
그렇다면 코사인함수를 이렇게 합성함수로 보면 어떨까요?
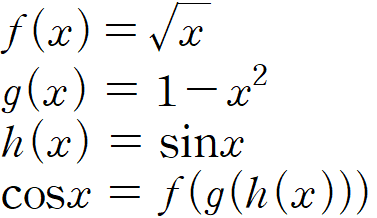
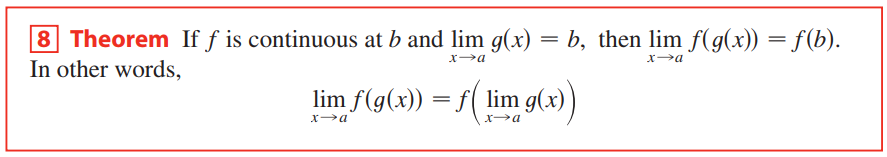
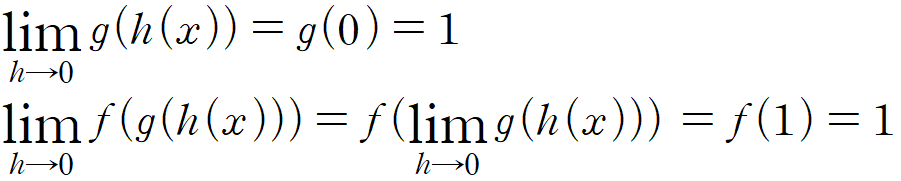
g는 0에서 연속이고, f는 1에서 연속이므로 무리 없이 가능합니다.
이렇게 cosh의 극한값이 1인게 우여곡절 끝에 증명됐습니다. 개인적으로 맘에 드네요.
드디어드디어
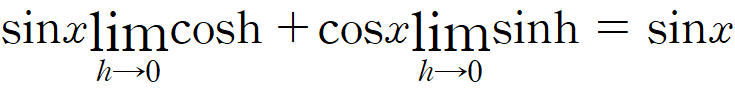
이 식이 모든 실수 x에 대해 참임을 증명했습니다.
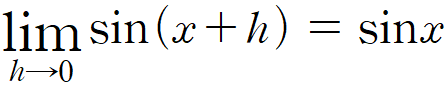
그리고 그건 이 식이랑 같은 의미라고 했었죠?
마침내 sinx는 정의역(실수 전체)에서 연속임이 밝혀졌습니다.
코사인이 정의역(실수 전체)에서 연속임을 보이러 갑시다. 이제 이건 쉽겠죠?

쉽네요.
이제 tanx가 정의역에서 연속임을 보일 건데,
그거 끌어씁시다 그거
곱의 연속 법칙.
tanx = sinx/cosx입니다.
tanx의 정의역에 속하는 모든 실수 a에 대해 다음이 만족됩니다.
- sinx는 a에서 연속이다.
- cosx는 a에서 연속이다.
- cos(a) ≠ 0.
또 어디서 많이 본 조건이죠? 곱의 연속 법칙을 사용할 수 있는 조건.
따라서 tanx는 정의역에 속하는 모든 실수 a에서 연속입니다.
tanx가 정의역에서 연속인 것도 보였습니다.
sec, csc, cot가 정의역에서 연속인 것은 패스하겠습니다. tanx가 정의역에서 연속인 것을 보일 때와 똑같습니다. 각각 1/cos, 1/sin, cos/sin이니깐요.
다음시간에는 제가 하고싶은 걸로 돌아오겠습니다.
아직 고등학생인 점
모든 풀이는 타이핑하면서 지어내는 뇌피셜인 점
으로 인해 오류가 있을 수 있으니 조언 감사히 받겠습니다.
또 질문 댓글 주시면 아는 선에서 최대한 답 드릴게요!
'Lecture > Calculus' 카테고리의 다른 글
| 미적분의 기본정리 2 증명 (F.T.C. 2) (0) | 2023.01.30 |
|---|---|
| 미적분의 기본정리 1 증명 (F.T.C. 1) (0) | 2023.01.29 |
| 평균값 정리 증명 (Mean Value Theorem) (0) | 2023.01.24 |
| 롤의 정리 증명 (Rolle's Theorem) (2) | 2023.01.23 |
| 페르마의 정리 증명 (Fermat's Theorem) + 최대, 극대, 임계값의 개념 (1) | 2023.01.23 |