평균값 정리는 순간변화율과 평균변화율을 매듭지으며, 다시 말해 도함수와 원시함수를 매듭짓습니다. 이는 수학적으로 의미가 큽니다. 실제로 다음번에 다룰 미적분학의 기본정리의 증명에서도 평균값 정리가 쓰입니다.
평균값 정리의 내용은 다음과 같습니다.

한글로 표현하자면 다음을 의미합니다.
함수 f가
- 닫힌구간 [a, b]에서 연속이며,
- 열린구간 (a, b)에서 미분가능하면
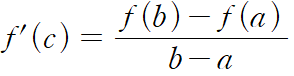
이를 만족하는 c가 (a, b)에 존재한다.
물론 양변에 b-a를 곱해 다르게 표현하면, f'(c)(b-a)=f(b)-f(a)를 만족하는 c가 (a, b)에 존재하는 것과도 같죠.
그럼 롤의 정리를 사용해 평균값 정리를 증명해보겠습니다.
점 A를 (a, f(a)), 점 B를 (b, f(b))라고 두겠습니다.
그러면 직선 AB의 방정식은 아래와 같이 표현됩니다.

이제 새로운 함수 h(x)를 아래와 같이 정의하겠습니다.

f(x)에서 직선 AB의 방정식을 뺀 꼴입니다. 즉 그래프적으로 표현하면 아래와 같은 상황이겠죠.
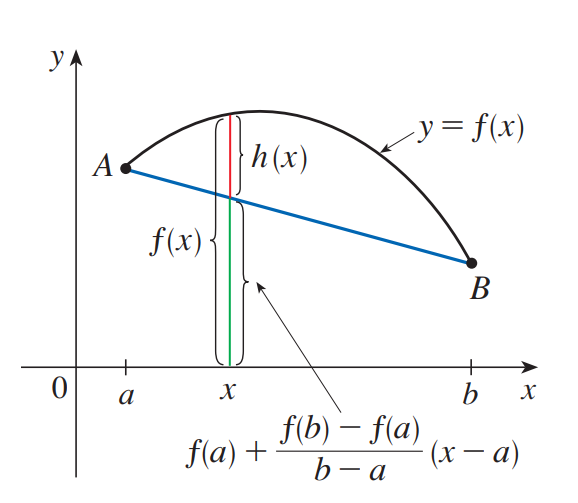
그러면 h(x)는 다음의 세 조건을 만족합니다.
- 함수 h는 [a, b]에서 연속이다. (∵ f가 연속이고, 직선의 방정식(일차함수)도 연속이므로, 이들의 차도 연속이다.)
- 함수 h는 (a, b)에서 미분가능하다. (∵ f가 미분가능하고, 직선의 방정식(일차함수)도 미분가능하므로, 이들의 차도 미분가능하다.
- h(a)=0, h(b)=0.(∵ 상단의 그래프를 통해 직관적으로 알 수 있고, 실제로 값을 대입해도 그렇다.)
한편 조건 2에서 함수 h가 미분가능하다고 했는데, 그 도함수는 아래와 같음을 쉽게 알 수 있습니다.

이제 롤의 정리를 사용할 수 있습니다. 앞서 함수 h가 만족함을 보였던 세 조건이 바로 롤의 정리의 조건입니다.
따라서 롤의 정리에 의해 h'(c)=0인 c가 (a, b)에 존재합니다.
그런데 조금 전 h'(x)의 식에 c를 대입하면, 바로 위의 문장은 다시 이렇게 표현할 수 있습니다.
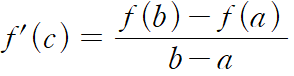
이렇게 말이죠.
어라, 증명이 끝나버렸습니다. 보시다시피 생각보다 간단합니다. 원리를 이해하면 증명은 외우기 쉽습니다. 롤의 정리의 조건을 기억하고 있다면, 평균값 정리의 조건이 왜 저렇게 되는지 알 수 있을 겁니다.
롤의 정리를 사용할 수 있도록, 그래프의 양 끝점을 잇는 직선을 원래 함수에서 뺌으로써, 양 끝점에서의 함숫값이 같은 새로운 함수를 만들어버리죠. 그래서 평균값 정리에서는 롤의 정리와 달리 구간 양 끝점에서의 함숫값이 같을 필요가 없습니다.
질문환영!ㅇ!
'Lecture > Calculus' 카테고리의 다른 글
| 미적분의 기본정리 1 증명 (F.T.C. 1) (0) | 2023.01.29 |
|---|---|
| 연속성의 정의와 관련 정리들의 증명 총정리 (1) | 2023.01.25 |
| 롤의 정리 증명 (Rolle's Theorem) (2) | 2023.01.23 |
| 페르마의 정리 증명 (Fermat's Theorem) + 최대, 극대, 임계값의 개념 (1) | 2023.01.23 |
| 극한 법칙의 엄밀한 증명(엡실론-델타 논법) - 합과 차의 법칙 (0) | 2023.01.23 |