페르마의 정리는 다음 글에 설명할 롤의 정리의 증명에 사용되며, 롤의 정리는 다시 미적분학에서 매우 중요한 정리 중 하나인 평균값 정리(MVT)의 증명으로까지 이어집니다. 따라서 이번 글에서 페르마의 정리의 증명을 다루겠습니다.

페르마의 정리는 위와 같습니다. f가 c에서 극댓값 혹은 극솟값을 가지며 f'(c)가 존재할 때, 그때의 f'(c) 값이 0이라는 뜻입니다.
이를 증명하기 이전에 극대/극솟값의 정의를 먼저 살피고, 페르마의 정리의 증명에 이용되는 최대·최소 정리까지 살펴봅시다.
먼저 최댓값과 최솟값(absolute maximum/minimum)은 말 그대로 함수의 정의역 전체에서 가장 크고 작은 값을 의미합니다.

Calculus에서는 위와 같이 설명하고 있습니다. D는 정의역입니다.
정의역에 속하는 모든 x에 대해 f(c)≥f(x)일 때 f(c)가 최댓값이고, 최솟값은 부호가 반대입니다.
반면 극댓값과 극솟값(local maximum/minimum)은 함수의 전체가 아닌 일부에서 가장 크고 작은 값을 의미합니다. 다시 말해, c가 극댓값을 가지면, x가 c 근처일 때(즉, c를 포함하는 어떤 열린구간에 x가 속할 때), f(c)≥f(x)입니다. 극솟값은 부호가 반대이고요.

이제 최대·최소 정리를 살펴보겠습니다. 간단히 말해, 닫힌구간 [a, b]에서 함수 f가 연속이면, f는 이 구간에서 최댓값과 최솟값을 갖는다는 의미입니다.

위와 같습니다. f(c)가 최댓값, f(d)가 최솟값입니다. 물론 c와 d는 [a, b]에 포함됩니다. 증명하려면 콤팩트성에 대해 다루어야 하므로 생략하겠습니다. 일단은 참이라고 가정합시다.
이제 페르마의 정리를 증명합시다. 우선 f가 c에서 극댓값을 가질 때를 증명하겠습니다.
f(c)가 극댓값이므로, h가 충분히 0에 가깝다면, 다음을 만족합니다.

물론 h의 부호와 무관하게 성립하는 식입니다.

앞선 식은 다시 위와 같이 표현할 수 있습니다.
이제 h의 부호에 따라 생각해보겠습니다.
h>0일 때에는, 다음이 성립합니다.

부등식의 양변에 h→0 극한(h>0이므로, 우극한)을 취하면

h<0일 때에는, 다음이 성립합니다.

부등식의 양변에 h→0 극한(h<0이므로, 좌극한)을 취하면

이를 만족합니다.
정리하자면, 다음 두 부등식이 만족됨을 알 수 있습니다.

그런데 f'(c)가 존재한다고 가정했으므로, 좌극한과 우극한은 같아야 합니다. 즉,

위의 등식이 성립해야 합니다.
f가 c에서 극솟값을 가질 때에도 증명 과정은 크게 다르지 않습니다.
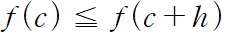
위와 같이 부등호가 반대 방향인 새로운 부등식을 얻을 수 있고, 이후로는 극댓값을 가질 때의 증명과 유사하게 이어가시면 되겠습니다.
한편 이때의 c는 임계값(critical number)이기도 합니다.
위 증명에서 등장한 c처럼 f'(c)=0를 만족하거나, 혹은 아예 f'(c)가 존재하지 않을 때, c를 임계값이라고 부릅니다. (c는 f의 정의역에 속해야 합니다.)
그러니까 페르마의 정리는,
f가 c에서 극댓값 혹은 극솟값을 가진다면, c는 f의 임계값이다.
라는 말로도 표현됩니다. f가 c에서 극댓값 혹을 극솟값을 가질 때,
f'(c)가 존재하지 않는다면 그 자체로 c는 임계값이고,
존재한다면 페르마의 정리에 의해 f'(c)=0이므로 역시나 c는 임계값입니다.
임계값의 개념을 알았으므로 어떤 구간에서의 최댓값과 최솟값을 찾는 법을 이제 살펴볼 수 있습니다.
닫힌 구간 [a, b]에서 연속인 함수 f의 최댓값을 찾으려면 다음 과정을 거치면 됩니다.
- 열린구간 (a,b)에서 f의 임곗값의 함숫값을 찾는다.
- 구간의 양 끝점의 함숫값(f(a)와 f(b))를 찾는다.
- 위에서 찾은 값 중 가장 큰 값이 최댓값, 가장 작은 값이 최솟값이다.
다음 글에서는 롤의 정리를 증명하겠습니다.
질문환영
'Lecture > Calculus' 카테고리의 다른 글
| 미적분의 기본정리 1 증명 (F.T.C. 1) (0) | 2023.01.29 |
|---|---|
| 연속성의 정의와 관련 정리들의 증명 총정리 (1) | 2023.01.25 |
| 평균값 정리 증명 (Mean Value Theorem) (0) | 2023.01.24 |
| 롤의 정리 증명 (Rolle's Theorem) (2) | 2023.01.23 |
| 극한 법칙의 엄밀한 증명(엡실론-델타 논법) - 합과 차의 법칙 (0) | 2023.01.23 |