미적분의 두 기본정리가 중요하다는 것을 또 짚고 넘어가지는 않겠습니다. 거두절미하고, 두 번째 정리는 아래와 같습니다.

첫 번째 정리는 부정적분에 대해서 설명했고,
두 번째 정리는 정적분에 대해 설명합니다.
이 정리는 역사적으로도 매우 뜻깊습니다. 어떤 구역의 넓이를 구한다는 것은 굉장히 중요한 일입니다. 고대 사회에서부터 이는 마찬가지였고, 토지의 넓이를 구하는 등의 이유로 말이죠. 그런데 과거에 넓이를 구했던 방법은, 현재로 치면 '구분구적법'에 가깝습니다.
구역을 매우 잘게 쪼개서, 그것들의 넓이를 모두 합하는 것이죠. 그 구역이 복잡한 형태였다면 더 힘들 일이 되었을 테고, 보다 정확한 넓이 계산을 위해서는 더 잘게 잘라야 하므로 보통 고역이 아니었습니다.
그런데 이제 적분이라는 개념이 등장합니다. 원시함수라는 것이 대두되죠. 이제는, 어떤 구간에서의 함수의 넓이를 구하기 위해 어떻게 함수를 쪼갤지 고민하는 것이 아니라, 함수의 원시함수가 무엇일지 고민하게 된 겁니다.
한편 이것은 마치 계차수열의 합과 다를 것이 없습니다. 예시를 봅시다.
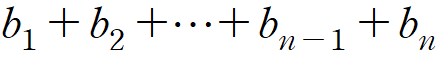
위와 같은 수열의 합은 어떻게 구해야 할까요? 수열에 대한 정보가 없으면 막막하기만 합니다. 이수열에 규칙이 없다면, 정말로 n번 더해봐야만 그 값을 알 수 있죠. 그런데 알고 보니 이 수열이 계차수열이었다면 어떨까요? 그러니까, 만약 아래와 같이 수열 aⁿ이 정의된다면요. (n은 아래첨자로 생각해주세욤)


미적분의 기본정리 2와 비슷한 형태이지 않나요?
b는 f에 대응되고, a는 f의 원시함수 F에 대응됩니다.
실제로, 도함수 f는 함수 F의 변화를 기술하고 있으며,
계차수열 bⁿ도 수열 aⁿ의 변화를 표현하고 있습니다.
원래 수열을 '알고만' 있다면, 계차수열의 합은 매우 쉽게 구할 수 있습니다. (앞서 봤듯, 끝 항에서 처음 항을 빼면 됩니다.)
원시 함수를 '알고만' 있다면, 함수의 정적분은 매우 쉽게 구할 수 있습니다. (F.T.C. 2에 의해, 끝 점에서의 원시함숫값에서 시작 점에서의 원시함숫값을 빼면 됩니다.)
이것이 미적분의 두 번째 기본 정리의 의의입니다. 이제부터 적분이라는 개념은 진정한 의미에서 수학이 됩니다.
증명하겠습니다.
들어가기에 앞서 다음 정리를 간단하게 증명하고 가겠습니다.
구간 [a, b]에서 연속이고 (a, b)에서 미분가능한 함수 h에 대해:
h'(x)=0이면, h는 상수함수이다.
고등학교 과정에서는 너무 당연한 말이지만, 그래도 증명 없는 정리는 없습니다. 가봅시다.

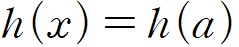
이것이 만족되므로, h(x)는 (a, x)에서 상수함수이고, 다시 x의 구간 내 최댓값이 b이므로 (a, b)에서 상수함수입니다.
이제 g를 아래와 같이 정의합시다.

자연스럽게 g'(x)=f(x)임을 알 수 있습니다.
그런데, 원시함수의 정의에 의해, F'(x)=f(x) 또한 성립합니다.
그러면, F'(x)-g'(x) = 0 이므로,
조금 전의 그 간단한 정리에 의해,
F(x)-g(x)가 상수함수임을 알 수 있습니다. 그 상수를 c라 놓고, F(x)-g(x)=c라 합시다.
그러면,
F(b)-F(a) = (g(b)+c) - (g(a)+c) = g(b)-g(a)인 것까지 알 수 있습니다.
그런데 g(a)는 0입니다.

이게 아까 전 g의 정의였는데, a에서부터 a까지의 적분이 0이라는 것은 정적분의 기본적인 성질이죠.
마침내, F(b)-F(a)=g(b)라는 사실을 알았습니다. 그리고 위에 정의된 g에 b를 대입하면,

'Lecture > Calculus' 카테고리의 다른 글
| 미적분의 기본정리 1 증명 (F.T.C. 1) (0) | 2023.01.29 |
|---|---|
| 연속성의 정의와 관련 정리들의 증명 총정리 (1) | 2023.01.25 |
| 평균값 정리 증명 (Mean Value Theorem) (0) | 2023.01.24 |
| 롤의 정리 증명 (Rolle's Theorem) (2) | 2023.01.23 |
| 페르마의 정리 증명 (Fermat's Theorem) + 최대, 극대, 임계값의 개념 (1) | 2023.01.23 |